Если вы не занимаетесь математикой или программированием, слово «алгоритм» может быть греческим для вас, но это один из строительных блоков всего, что вы используете для чтения этой статьи. Вот краткое объяснение того, чем они являются и как они работают.
Отказ от ответственности: я не учитель математики или компьютерных наук, поэтому не все термины, которые я использую, являются техническими. Это потому, что я пытаюсь объяснить все на простом английском языке для людей, которые не совсем знакомы с математикой. Это сказанное, есть некоторая математика, вовлеченная, и это неизбежно. Математические гики, не стесняйтесь исправлять или лучше объяснять в комментариях, но, пожалуйста, сделайте это простым для математически отвергнутых среди нас.
Изображение Иэн Руотсала
Что такое алгоритм?
Слово «алгоритм» имеет этимологию, аналогичную «алгебре», за исключением того, что это относится к самому арабскому математику аль-Хорезми (просто интересный трюк). Алгоритм для нас, не являющихся программистами, представляет собой набор инструкций, которые принимают входные данные A и предоставляют выходные данные B, которые каким-то образом изменяют данные. Алгоритмы имеют широкий спектр применения. В математике они могут помочь вычислить функции из точек в наборе данных, среди гораздо более сложных вещей. Помимо их использования в самом программировании, они играют важную роль в таких вещах, как сжатие файлов и шифрование данных.
Базовый набор инструкций
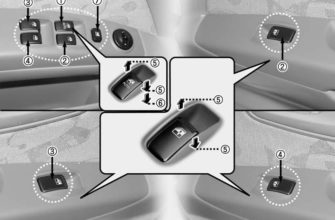
Допустим, ваш друг встречает вас в продуктовом магазине, и вы ведете его к себе. Вы говорите такие вещи, как «заходите через правые двери», «проходите через раздел рыбы слева» и «если вы видите молочную ферму, вы прошли мимо меня». Алгоритмы работают так. Мы можем использовать блок-схему, чтобы проиллюстрировать инструкции на основе заранее известных нам критериев или выяснить их в процессе.

(изображение под названием «Ледокольный режим» РЕДАКТИРОВАТЬ: любезно предоставлено Trigger и Freewheel)
От START вы бы пошли по пути, и в зависимости от того, что происходит, вы следуете «потоку» до конечного результата. Блок-схемы являются визуальными инструментами, которые могут более понятно представлять набор инструкций, используемых компьютерами. Точно так же алгоритмы помогают делать то же самое с более математическими моделями.
диаграммы
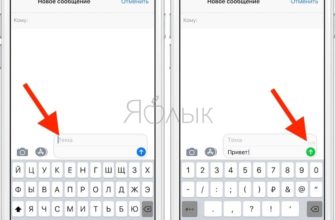
Давайте использовать график, чтобы проиллюстрировать различные способы, которыми мы можем дать указания.

Мы можем выразить этот граф как связь между всеми его точками. Чтобы воспроизвести это изображение, мы можем дать набор инструкций кому-то еще.
Метод 1
Мы можем представить это как ряд точек, и информация будет соответствовать стандартной форме графа = {(x1, y1), (x2, y2),…, (xn, yn)}.
график = {(0,0), (3,0), (3,3), (5,5), (7,10), (8,7), (9,4), (10,1) }
Довольно легко построить каждую точку, одну за другой, и соединить их с предыдущей точкой. Однако представьте себе граф с тысячами точек или несколькими сегментами, которые идут в разные стороны. В этом списке будет много данных, верно? И тогда необходимость соединять каждого, по одному, может быть болью.
Метод 2
Другая вещь, которую мы можем сделать, это дать начальную точку, наклон линии между ней и следующей точкой, и указать, где ожидать следующую точку, используя стандартную форму графика = {(начальная точка}, [m1, x1, h1 ],…, [Mn, xn, hn]}. Здесь переменная «m» представляет наклон линии, «x» представляет направление для подсчета (x или y), а «h» говорит вам, как многие считают в указанном направлении. Вы также можете помнить наносить точку после каждого движения.
graph = {(0,0), [0, x, 3], [0, y, 3], [1, x, 2], [2.5, x, 2], [-3, x, 1], [-3, х, 1], [-3, х, 1]}
Вы получите тот же график. Вы можете видеть, что последние три термина в этом выражении одинаковы, поэтому мы можем сократить это, просто сказав «повторить это три раза» каким-то образом. Допустим, каждый раз, когда вы видите переменную «R», это означает, что нужно повторить последнее. Мы можем это сделать:
graph = {(0,0), [0, x, 3], [0, y, 3], [1, x, 2], [2.5, x, 2], [-3, x, 1], [R = 2]}
Что если отдельные точки не имеют большого значения, а только сам график? Мы можем объединить эти последние три раздела следующим образом:
graph = {(0,0), [0, x, 3], [0, y, 3], [1, x, 2], [2.5, x, 2], [-3, x, 3]}
Это немного сокращает вещи от того, где они были раньше.
Метод 3
Давайте попробуем сделать это по-другому.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
y = 2,5x-7,5, 5≤x≤7
y = -3x + 29, 7≤x≤8
y = -3x + 29, 8≤x≤9
y = -3x + 29, 9≤x≤10
Здесь мы имеем это в чисто алгебраических терминах. Еще раз, если сами точки не имеют значения, а имеет значение только график, мы можем объединить последние три элемента.
y = 0, 0≤x≤3
x = 0, 0≤y≤3
y = x, 3≤x≤5
у = 2.5x-7.5, 5≤x≤7
y = -3x + 29, 7≤x≤10
Теперь, какой метод вы выберете, зависит от ваших способностей. Возможно, вы хорошо разбираетесь в математике и графике, поэтому вы выбираете последний вариант. Возможно, вы хорошо разбираетесь в навигации, поэтому выбираете второй вариант. Однако в области компьютеров вы выполняете множество различных задач, и возможности компьютера на самом деле не меняются. Поэтому алгоритмы оптимизированы для задач, которые они выполняют.
Еще один важный момент, который следует отметить, заключается в том, что каждый метод основан на ключе. Каждый набор инструкций бесполезен, если вы не знаете, что с ними делать. Если вы не знаете, что должны наносить на карту каждую точку и соединять точки, первый набор точек ничего не значит. Если вы не знаете, что означает каждая переменная во втором методе, вы не будете знать, как их применять, как ключ к шифру. Этот ключ также является неотъемлемой частью использования алгоритмов, и часто этот ключ можно найти в сообществе или с помощью «стандарта».
Сжатие файлов
Когда вы загружаете файл .zip, вы извлекаете содержимое, чтобы вы могли использовать все, что находится внутри него. В настоящее время большинство операционных систем могут погружаться в файлы .zip как обычные папки, делая все в фоновом режиме. На моем компьютере с Windows 95 более десяти лет назад мне пришлось извлечь все вручную, прежде чем я увидел что-то большее, чем имена файлов внутри. Это потому, что то, что хранилось на диске в виде файла .zip, было недоступно для использования. Подумайте о раскладном диване. Если вы хотите использовать его как кровать, вы должны снять подушки и развернуть, что займет больше места. Когда вам это не нужно или вы хотите транспортировать его, вы можете сложить его обратно.
Алгоритмы сжатия настраиваются и оптимизируются специально для типов файлов, на которые они ориентированы. Например, каждый из аудиоформатов использует свой способ хранения данных, который при декодировании с помощью аудиокодека дает звуковой файл, аналогичный исходному сигналу. Для получения дополнительной информации об этих различиях, ознакомьтесь с нашей предыдущей статьей, Каковы различия между всеми этими аудиоформатами? Аудиоформаты без потерь и файлы .zip имеют одну общую черту: они оба дают исходные данные в точном виде после процесса распаковки. Аудиокодеки с потерями используют другие средства для экономии места на диске, такие как обрезка частот, которые не могут быть услышаны человеческими ушами, и сглаживание формы волны в секциях, чтобы избавиться от некоторых деталей. В конце концов, хотя мы, возможно, не сможем действительно услышать разницу между дорожками MP3 и CD, в первом случае определенно существует дефицит информации.
Шифрование данных

Алгоритмы также используются при защите данных или линий связи. Вместо того, чтобы хранить данные, чтобы они занимали меньше места на диске, они хранятся таким образом, который не обнаруживается другими программами. Если кто-то украдет ваш жесткий диск и начнет его сканировать, он сможет забрать данные, даже если вы удалите файлы, потому что сами данные все еще там, даже если местоположение для пересылки на них больше нет. Когда данные зашифрованы, все, что хранится, не похоже на то, что есть. Обычно это выглядит случайным образом, как будто фрагментация накапливалась со временем. Вы также можете хранить данные и отображать их как файлы другого типа. Графические файлы и музыкальные файлы хороши для этого, так как они могут быть довольно большими, не вызывая подозрений, например. Все это делается с помощью математических алгоритмов, которые принимают какой-то вид ввода и преобразуют его в другой, очень специфический тип вывода. Для получения дополнительной информации о том, как работает шифрование, ознакомьтесь с объяснениями HTG: что такое шифрование и как оно работает?
Алгоритмы являются математическими инструментами, которые обеспечивают различные применения в информатике. Они работают, чтобы обеспечить путь между начальной точкой и конечной точкой согласованным образом, и предоставляют инструкции для ее следования. Знаете больше, чем мы отметили? Поделитесь своими объяснениями в комментариях!